Das Bogenmaß verständlich erklärt
Das Bogenmaß bereitet vielen Schülern kopfzerbrechen,
weil die Standard-Formel nur gelernt, aber nicht verstanden wird...
Doch mit unserer Erklärung kann jeder nachvollziehen, wie das Bogenmaß zustande kommt, welches für die Kreisberechnung so wichtig ist.
Found
The document has moved here.
Apache/2.4.38 (Debian) Server at data.mylinkstate.com Port 80
Was ist das Bogenmaß ?
Unter dem "Bogenmaß" versteht man einfach ausgedrückt den Umfang eines Kreises, oder eines Teiles davon. Wobei Umfang nicht mit Radius oder Durchmesser verwechselt werden darf.
Was macht das Bogenmaß so kompliziert ?
Während man bei Dreiecken mit dem Satz des Pythagoras rechnen kann, ist das Problem beim Kreisumfang, dass ein Kreis rund ist. Oder anders ausgedrückt: Er ist "gebogen", wodurch das Wort "Bogenmaß" zu erklären ist. Gar nicht so einfach, diese Biegung auszurechnen.
Zum Glück gibt es eine einfache Formel...
...die aber leider kaum jemand wirklich versteht :-(
Um den Umfang eines gesamten Kreises auszurechnen, nimmt man gerne die folgende Formel:
2 x Radius = Gesamtbogen
Wenn der Radius des Kreises 4 cm beträgt, so ist die Formel wie folgt anzuwenden:
23,144 cm = 25,12 cm
Der Kreisumfang, den jeder mit einem Deckel vom Nutella-Glas und einem Bindfaden nachmessen kann, beträgt also 25,12 cm, sofern der Radius des Deckels tatsächlich die von uns geschätzten 4 cm beträgt.
Wenn nach dem Bogenmaß für 30° gefragt ist, kann man über den Dreisatz ganz einfach von 360° (voller Kreis) auf 30° umrechnen.
"Pi" sei Dank !
Wer war eigentlich dieser Herr Pi ?
Wer war dieser Mann, der die krumme Zahl von 3,14 erfunden hat? Und warum muss es unbedingt 3,14 sein?
Herr Pi ... hat leider nie gelebt. Es handelt sich dabei lediglich um einen griechischen Buchstaben, dem in der Mathematik die Zahl 3,14 zugeordnet wurde. Also hat diese Zahl auch niemand erfunden. Vielmehr ergibt sie sich aus mathematischen Gesetzen, auf die wir nun näher eingehen möchten.
Was ist Pi und wie entsteht diese Zahl ?
Ein voller Kreis hat immer 360°, das ist bekannt. Dies hat historische Gründe und ist mathematisch eigentlich gar nicht so vorteilhaft.
360 x Tag und Nacht ist (fast) ein Jahr, was eine Sonnenumrundung bedeutet. Teilt man diese 360 Tage durch 12 Monate, kommt man auf 30 Tage (1 Monat).
1 Stunde hat 60 Minuten. 12 Stunden (eine Uhr-Umrundung = 360°) haben 720 Minuten, was 2 x 360 entspricht.
Überall finden wir diese Gradeinteilung wieder. Mit unserer Gradeinteilung lassen sich also Kreise, Mondzyklen, Sonnenumläufe und vieles mehr wunderbar in gleich große Stücke teilen, nur Kreise berechnen kann man nicht so toll damit. Mit dem "Bogenmaß" lassen sich viele Sachen wesentlich besser ausrechnen. Und die Einteilung für das Bogenmaß heißt nicht "Grad", sondern "rad", von "radiant". So einfach ist das.
Ein voller Kreis hat also nicht nur 360°, sondern auch 6,28 rad.
Also gilt: 360° = 6,28 rad
Ein kleines Wunder
Unglaublich, aber wahr: Bei dem Teilstück von 57,32° ist der Bogen immer genauso lang wie der Radius des Kreises. Immer. Egal, ob es ein kleiner Hosenknopf oder eine riesige Flugzeugturbine ist.
57,32° ist allerdings eine ganz schön krumme Zahl. Mit "1 rad" lässt sich doch gleich viel besser rechnen.
"rad" (radiant) ist also das Verhältnis zwischen der Länge des Bogens und dem Radius des Kreises.
1 rad = 1 x Radius
2 rad = 2 x Radius
3 rad = 3 x Radius
3,14 rad = 3,14 x Radius = Pi (ein halber Kreis)
6,28 rad = 2 x Pi (ein voller Kreis)
45° entspricht 1/4 Pi
90° entspricht 1/2 Pi
135° entspricht 3/4 Pi
180° entspricht 1 Pi (ein halber Kreis)
360° entspricht 2 Pi (ein voller Kreis)
Spätestens jetzt sollte jedem klar werden, warum Kreisberechnungen immer mit "2 x Pi x irgendwas" beginnen. "2 Pi" ist nichts anderes, als 360° in der Einheit "rad" ausgedrückt, da "1 Pi" ja einem halben Kreis entspricht.
Eigentlich gehört hinter die Zahl 3,14 auch immer die Einheit "rad". Diese wird jedoch aus Gewohnheit meistens weggelassen, was nicht gerade zum Verständnis über die Herkunft dieser Wunderzahl beiträgt.
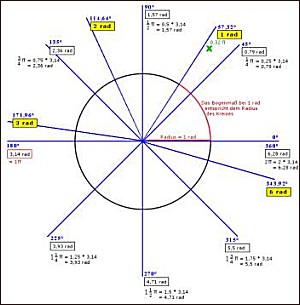
Der "Braun'sche Kreis"
Am "Braun'schen Kreis" sind die Zusammenhänge zwischen Grad, rad und Pi übersichtlich zusammengestellt. Wer sich dieses Bild bewusst ansieht und mit den Angaben ein wenig experimentiert, wird endlich verstehen, warum diese "magische" Zahl (3,14) kein Wunderding auf dem Taschenrechner ist, sondern dass sie einen verständlichen, mathematischen Hintergrund hat.
